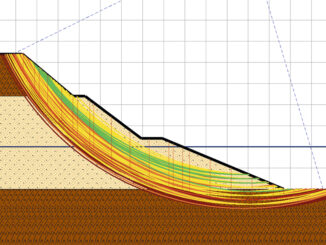
Евгений Яшков, технический специалист Micromine Origin
Для оценки содержаний в блочных моделях в ГГИС Micromine Origin & Beyond используются несколько методов интерполяции: метод обратных расстояний и кригинг в нескольких его разновидностях. И если метод обратных расстояний обладает предельно прозрачной математикой, которую легко воспроизвести и вручную на тетрадном листке, то с кригингом дела обстоят сложнее. Многие специалисты знают про преимущества кригинга, но не знают про внутреннее устройство алгоритма оценки. Попытка прояснить ситуацию зачастую приводит наши поиски к сложной специализированной литературе, наполненной формулами и академическими терминами.
В данной статье мы постараемся разобрать, как устроен кригинг, на примере одного из самых распространенных его вариантов — ординарного кригинга.
Как и все методы оценки, кригинг требователен к подготовке данных опробования. Для получения качественного результата пробы должны быть декластеризованы, разбиты на геологические домены и на популяции с нормальным (логнормальным) распределением, ураганные содержания должны быть подавлены. В Micromine Origin & Beyond есть все необходимые инструменты для предварительного статистического анализа проб, автоматического разбиения на популяции, урезки ураганов, композитирования и подготовки моделей вариограмм.
Кригинг относится к линейным методам оценки. «Линейный» означает, что для интерполяции используются непосредственно сами содержания проб без каких-либо преобразований и их весовые коэффициенты.
Зная это, можно представить себе формулу кригинга в простейшем виде:
оцененное содержание в блоке = сумма (содержание пробы * вес пробы)
Таким образом, оцененное содержание в блоке равняется сумме произведений содержаний проб, участвующих в оценке, и их весовых коэффициентов.
Очень похоже на формулу оценки методом обратных расстояний, не так ли? Действительно, в этом оба метода сходятся. Различаются же они способом нахождения весовых коэффициентов проб. Если в методе обратных расстояний вес определяется путем нахождения обратной степени (чаще всего обратного квадрата) от расстояния между пробой и оцениваемой точкой, то в кригинге используется более сложный метод расчета, позволяющий лучше учесть особенности распределения данных.
В основе определения весов проб в кригинге лежат два принципа:
— наименьшая разница между фактическими и оцененными содержаниями (минимизация дисперсии погрешности);
— отсутствие погрешности (несмещенность оценки).
Что означают эти принципы?
Наименьшая разница между фактическими и оцененными содержаниями, также называемая минимизацией дисперсии погрешности, означает, что при оценке содержаний веса проб должны быть подобраны таким образом, чтобы снизить к минимуму разницу между оцененным содержанием и фактическим содержанием в оцениваемой точке:
(содержание в пробе * вес пробы — фактическое содержание)2 нужно свести к минимуму
Отсутствие погрешности, также называемое несмещенностью оценки, означает, что сумма весов всех проб, участвующих в оценке, должна быть равна единице: это условие позволяет избежать завышения или занижения оцененных содержаний.
У читателя может возникнуть вопрос: откуда нам узнать фактическое содержание в точке, которую мы только собираемся оценить? Именно здесь метод кригинга и задействует вариограмму. Вариограммы рассчитываются на основе сравнения пар фактических значений в пробах, поэтому можно сказать, что они несут информацию о фактических содержаниях.
Рассмотрим работу метода кригинга на простом примере.
Зная содержания трех входных проб, пронумерованных с 1 до 3, оценим содержание в блоке с использованием ординарного кригинга.
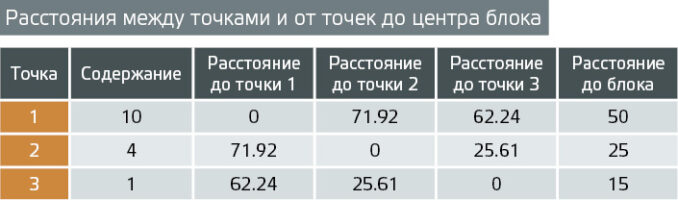
Как и в методе обратных расстояний, первым шагом измеряется расстояние от оцениваемой точки до каждой входной пробы, помимо этого, в кригинге также измеряются расстояния между самими пробами (см. рис. 1).
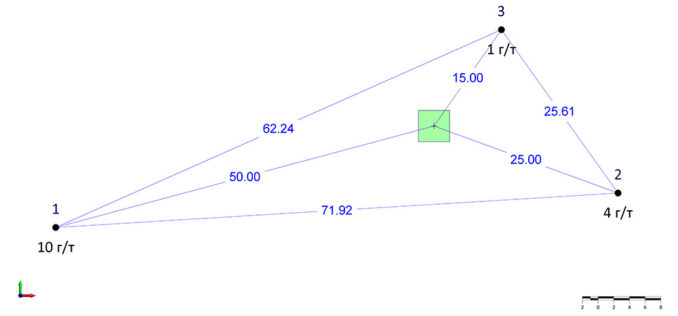
Содержания в точках и расстояния между точками и от точек до центра блока (к рис. 1)
Далее на основании заранее построенных моделей вариограмм вычисляются значения вариограмм для каждого из расстояний. По сути, модель вариограммы в данном случае выступает в роли «таблицы подстановок», по которой мы определяем значение вариограммы, соответствующее определенному расстоянию.
Если распределение содержаний в исследуемой области является анизотропным, используются три модели направленных вариограмм. Значение вариограммы для каждого расстояния при этом определяется по модели, которая вычисляется на основании положения осей вариограмм и направления, по которому было измерено расстояние (рис. 2).
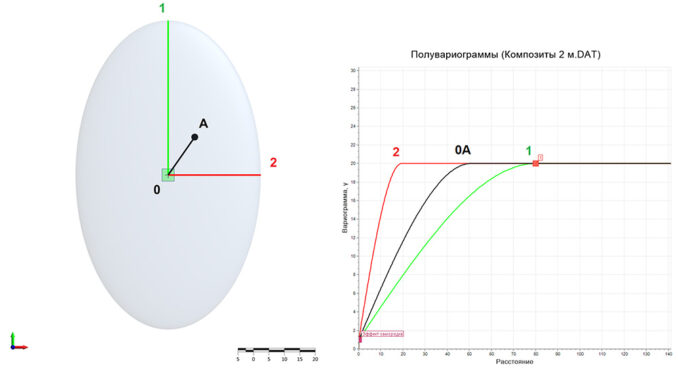
В данном примере рассматривается ситуация с изотропным распределением: значения вариограмм вычисляются на основании одной всенаправленной модели вариограммы (рис. 3).
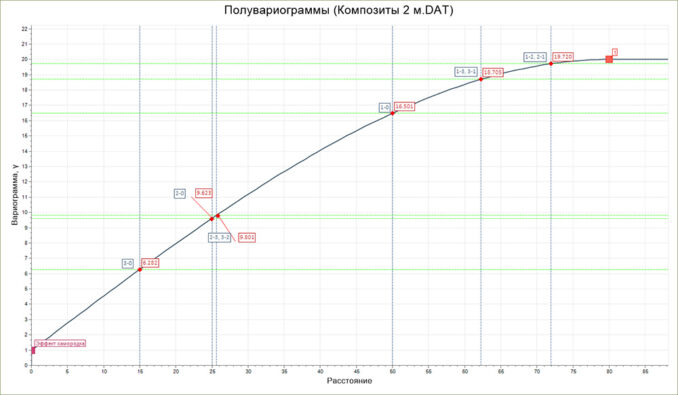
Измеренные расстояния и соответствующие им значения вариограммы (к рис. 3)
Веса проб рассчитываются по системе линейных уравнений, где γ(x11), γ(x12), γ(xnn) — значения вариограмм для рассчитанных расстояний между пробами, λ1, λ2… λn — весовые коэффициенты, которые необходимо найти, γ(x10), γ(x20)… γ(xn0) — значения вариограмм для рассчитанных расстояний между пробами и центроидом блока, μ — множитель Лагранжа.
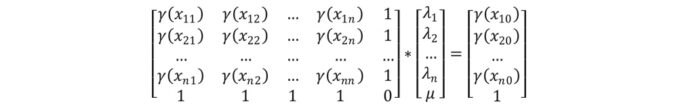
Для оценки содержания по трем пробам с известными значениями система уравнений будет иметь вид:
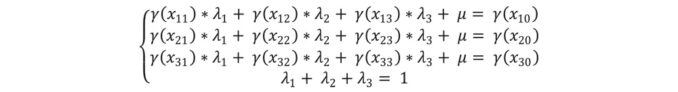
На секунду вернемся к принципам кригинга. Первые три уравнения (по одному на каждую из проб) в данной системе отвечают за первый принцип — наименьшую разницу между фактическими и оцененными содержаниями. Поскольку у нас нет возможности заранее знать фактическое содержание в оцениваемой точке, в уравнении участвуют не содержания, а значения вариограмм.
Последнее уравнение всегда отвечает за второй принцип — несмещенность оценки: сумма весов равняется единице.
После подстановки вычисленных значений вариограмм система уравнений будет иметь вид:
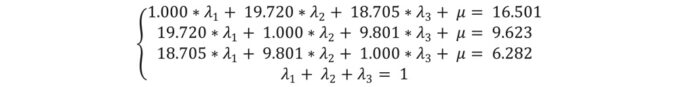
В результате решения уравнения рассчитываются следующие весовые коэффициенты:
λ1 = 0.159 λ3 = 0.601
λ2 = 0.240 μ = 0.361
Множитель Лагранжа в дальнейшей оценке не участвует.
Подставляем весовые коэффициенты и содержания проб в основное уравнение кригинга:
Au(x0 )=Au(x1 )*λ1+Au(x2 )*λ2+Au(x3 )*λ3
Au(x0 )=10*0.159+4*0.240+1*0.601
Содержание в блоке будет равняться 3.151.
Таким образом, при внутреннем рассмотрении метод Кригинга оказывается простым и прозрачным. На достоверность оценки содержаний этим методом в первую очередь влияет качество подготовки моделей вариограмм. В свою очередь, качество подготовки вариограмм зависит от грамотной обработки вводных данных опробования.
Надеюсь, данная статья помогла вам лучше понять суть оценки содержаний методом кригинга и сделала этот процесс более прозрачным для вас. А с построением вариограмм и расчетами вам поможет ГГИС Micromine Origin & Beyond.